Lernziele
Hinweis: Wir behandeln keine Umwandlungen, die grösser als zwei Byte oder 65’53510 sind.
- Sie können Binärzahlen und Hexadezimalzahlen in 4-Bit-Paketen ineinander umwandeln.
- Sie wissen, wie das RGB-Farbmodell funktioniert.
- Sie wissen, was beispielsweise 3-Bit-Farbtiefe pro Kanal bedeutet und wie viele Farben man daraus mischen kann.
- Sie verstehen die Inhalte des Theorieeintrags
Hexadezimal: Zahlen mit Buchstaben?
Stellen Sie sich nun einmal einen Computerspeicher mit mehreren Bytes vor: Natürlich können wir Menschen nichts damit anfangen.
Gäbe es nicht ein Zahlensystem, dass so einfach zu lesen wäre wie das Dezimalsystem, aber die Binärzahlen besser repräsentiert?
Führen Sie sich vor Augen, dass ein Byte zweimal 4 Bit hat. Wie viele verschiedene Zahlen können Sie mit 4 Bit darstellen? Die grösste Zahl ist 11112 = 1510, und dazu noch 0. Das sind, wenig erstaunlich, 24 = 16 verschiedene Zahlen. Hätten wir doch ein Zahlensytem, das 16 als Basis hätte…
Schaffen wir uns unser Glück doch selbst und kreieren ein Zahlensystem, dass 16 als Basis hat! Natürlich haben wir zu wenig Symbole dafür, weil wir im Dezimalsystem leben. Aber nehmen wir einfach Buchstaben. Jetzt achten Sie darauf, wie elegant dieses “hexadezimale” 16er-Zahlensystem aufs binäre Zahlensystem passt:
| Hexadezimal | Binär | Dez |
|---|---|---|
| 0 | 0000’0000 | 0 |
| 1 | 0000’0001 | 1 |
| 2 | 0000’0010 | 2 |
| 3 | 0000’0011 | 3 |
| 4 | 0000’0100 | 4 |
| 5 | 0000’0101 | 5 |
| 6 | 0000’0110 | 6 |
| 7 | 0000’0111 | 7 |
| 8 | 0000’1000 | 8 |
| 9 | 0000’1001 | 9 |
| A | 0000’1010 | 10 |
| B | 0000’1011 | 11 |
| C | 0000’1100 | 12 |
| D | 0000’1101 | 13 |
| E | 0000’1110 | 14 |
| F | 0000’1111 | 15 |
| 10 | 0001’0000 | 16 |
| 11 | 0001’0001 | 17 |
| 12 | 0001’0010 | 18 |
| 13 | 0001’0011 | 19 |
| 14 | 0001’0100 | 20 |
| 15 | 0001’0101 | 21 |
| 16 | 0001’0110 | 22 |
| 17 | 0001’0111 | 23 |
| 18 | 0001’1000 | 24 |
| 19 | 0001’1001 | 25 |
| 1A | 0001’1010 | 26 |
| 1B | 0001’1011 | 27 |
| 1C | 0001’1100 | 28 |
| 1D | 0001’1101 | 29 |
| 1E | 0001’1110 | 30 |
Wunderbar! Eine Ziffer aus dem Hexadezimalsystem ist genau vier Bit lang! Das heisst:
- Sie können ein Byte immer in genau zwei Hex-Ziffern ausdrucken.
- Anders als beim Dezimalsystem können Sie beide Hex-Ziffern getrennt umwandeln.
Zusammenfassung Binär, Dezimal, Hexadezimal
Den Theorieeintrag erstellen wir zusammen in Onenote. Wir lernen:
- Umrechnen hexadezimal zu dezimalen mit der Summenschreibweise.
- Umrechnen dezimal zu hexadezimal mit:
- Divisionsmethode
- Zerlegen in Potenzen
- Umrechnen binär zu hexadezimal in 4-Bit-Paketen
- Umrechnen hex zu binär in 4-Bit-Paketen
Farben in RGB
Gratulation! Jetzt haben Sie das Rüstzeugs, ein grundlegendes Konzept zu verstehen, das Sie täglich umgibt: Farben und Farbmodelle!
Wenn Sie Ihren Bildschirm aus der Nähe anschauen, merken Sie, dass sie aus kleinen, farbig leuchtenden Stellen bestehen. Hier eine Nahaufnahme von Wikipedia:
Wie LCDs genau farbiges Licht erzeugen ist sehr interessant! Falls Sie das interessiert, hier ein Youtube-Video dazu. Aber Sie können die Informatik problemlos verstehen, ohne die Physik davon überhaupt anzuschauen.
Diese “Lämpchen” sind rot, dann grün, dann blau, und dann wieder rot, grün, blau, und so weiter. Ein Dreierpack aus einem roten, grünen und blauen “Lämpchen” ist ein RGB-Pixel.
RGB-Pixel haben also mindestens folgende Charakteristiken:
- Werte für Rot, Grün, Blau
- Koordinaten
Farbtiefe
Stellen Sie sich mal vor, wir könnten diese RGB-Lämpchen einfach nur ganz ein- oder ausschalten. Wie viele Mischfarben könnten wir erzeugen?
Lösung
Um es sich einfach zu machen, können Sie sich in diesem Beispiel einen RGB-Pixel als eine einzelne Binärzahl vorstellen.
- 0002 wäre schwarz.
- 0012 wäre blau.
- 0102 wäre grün.
- 0112 wäre die Mischung aus grün und blau, also hellblau.
⋮- 1112 wäre die Mischung aller Farben, also weiss.
Wie viele Kombinationen gibt es also? 1112 sind 710, aber da wird 0002 (Schwarz) nicht mitgezählt. Zusammen mit Schwarz gibt es 8 Farbkombinationen, also 23.
Ohne Weiss und Schwarz sähe der Regenbogen dann so aus:
Typischerweise reicht die Werte für Rot, Grün und Blau von 0 bis 255… Diese Zahl sollte Ihnen bekannt vorkommen.
- Was sagt Ihnen das über die Datenstruktur aus?
- Wie viele Mischfarben können Sie daraus erzeugen?
Lösung
255 ist die höchste Zahl, die Sie in einem Byte (also 8 Bit) speichern können. Das heisst: Jeder Farbkanal hat pro Pixel 8 Bit zu Verfügung, um eine Zahl zu speichern.
Als wir noch 1 Bit pro Kanal hatten, hatten wir pro Kanal 2 Zustände (21) und deswegen 23 Farbkombinationen. Daraus erschliesst sich:
Farbkombinationen = Zustände pro KanalAnzahl Kanäle
Jetzt haben wir pro Kanal 28 = 256 Zustände pro Kanal (inkl. Null!). Bei drei Kanälen haben wir also 2563 Kombinationen. Das gibt: 16’777’216 Farben!
Sie sehen also: Je nachdem wie viel Informationen Sie pro Farbkanal haben, desto mehr Mischfarben können Sie erzeugen. Das nennt man die Farbtiefe, die typischerweise in Bit angegeben wird (“8 bits/channel” = eine Farbtiefe von 8 Bit).

Wieso Farbtiefe? Weil Sie sich ein Bild nun als Quader vorstellen können.
- Die Anzahl Pixel in der Breite ist die Breite.
- Die Anzahl Pixel in der Höhe ist die Höhe.
- Die Farbtiefe × Anzahl Kanäle ist die Tiefe.
Die Datenmenge, die Sie benötigen, um das Bild zu speichern, ist dann einfach das Volumen des Quaders.
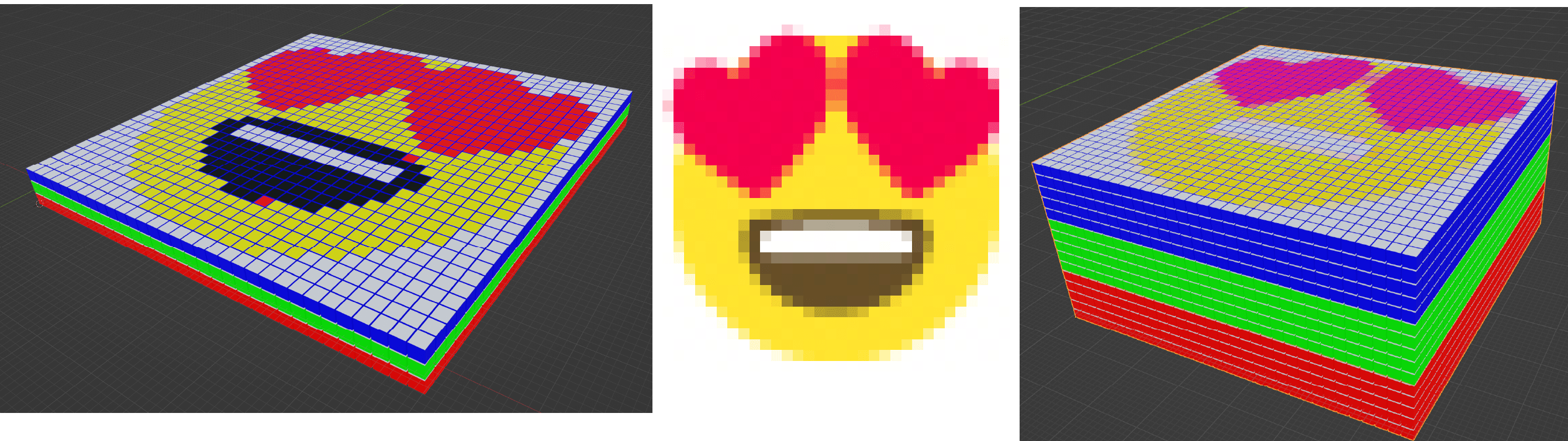
Wenn Sie wenig Farbtiefe haben, haben Sie wenig Mischfarben, aber auch weniger Daten. Ich habe Ihnen das hier zu visualisieren versucht.
- Links haben Sie 1 Bit Farbtiefe - und deswegen nur wenige Farben.
- Rechts haben Sie 4 Bit Farbtiefe - und deswegen sehen Sie mehr Farbschattierungen, aber haben auch einen grösseren Block von Daten.
Im Webdesign werden eben diese Ideen verwendet, um Farben zu mischen. Verändern Sie mal die Hintergrundfarbe des Informatikgartens und versuchen Sie, die Farbnotation mit Hashtag ”#” zu verstehen!
Aufgabe zu Farbtiefe & Datenmenge
Wie viele Bytes an Daten brauchen Sie, wenn Sie ein unkomprimiertes RGB-Bild von 1000 Pixel Breite, 1000 Pixel Höhe und mit 8 Bit Farbtiefe speichern wollen?
Zusammenfassung
Theorie: Pixel & Farbtiefe
Bei Bildern ist die kleinste Einheit ein Pixel. Ein Pixel besteht typischerweise aus:
- Einer Zahl pro Farbkanal (drei bei RGB, eine bei Graustufe)
- Zwei Koordinaten für x und y
Ein RGB-Bild mit 8 Bit Farbtiefe pro Farbkanal kann rund 16,8 Millionen Farben mischen, weil:
- 8-Bit pro Kanal ⇒
- 256 verschiedene Zustände pro Kanal ⇒
- 2563 Kombinationen insgesamt ⇒
- 16,8 Millionen Kombinationen
8-Bit-RGB wird typischerweise dezimal oder hexadezimal notiert. Ein schönes Orange wäre z.B.:
rgb(255, 64, 16)#ff4010.Das ist zweimal die gleiche Farbe, weil:
- Rot: 25510 = ff16
- Grün: 6410 = 4016
- Blau: 1610 = 1016



