Agent-Based Modelling mit NetLogo
Bisher haben wir Populationen mit mathematischen Gleichungen modelliert. Wir haben Formeln verwendet, die beschreiben, wie sich eine Gesamtpopulation über die Zeit entwickelt. Das funktioniert gut für einfache Szenarien, aber was passiert, wenn wir komplexere Systeme verstehen wollen - zum Beispiel das Zusammenspiel von Jägern und Beute?
Was ist Agent-Based Modelling?
Agent-Based Modelling (ABM) ist ein völlig anderer Ansatz: Statt die Population als Ganzes zu berechnen, simulieren wir jedes einzelne Individuum (genannt “Agent”).
| Mathematisches Modell | Agent-Based Modell |
|---|---|
| Berechnet Gesamtpopulation | Simuliert jedes Individuum |
| ”Top-down” Ansatz | ”Bottom-up” Ansatz |
| Formel: | Jeder Wolf entscheidet selbst |
| Alle Wölfe sind gleich | Jeder Wolf kann anders sein |
| Schnelle Berechnung | Aufwändige Simulation |
Das Prinzip
Jeder Agent folgt einfachen Regeln:
Schafe:
- Bewegen sich zufällig über das Feld
- Fressen Gras, wenn sie auf einem grünen Feld stehen → gewinnen Energie
- Reproduzieren sich mit einer gewissen Wahrscheinlichkeit
- Verlieren Energie bei jeder Bewegung
- Sterben, wenn ihre Energie auf 0 sinkt - oder sie gefressen werden, natürlich
Wölfe:
- Bewegen sich zufällig über das Feld
- Fressen ein Schaf, wenn sie auf dem gleichen Feld stehen → gewinnen Energie
- Reproduzieren sich mit einer gewissen Wahrscheinlichkeit
- Verlieren Energie bei jeder Bewegung
- Sterben, wenn ihre Energie auf 0 sinkt
Aus diesen einfachen Einzelregeln entsteht das emergente Verhalten des Gesamtsystems - Populationsdynamiken, die wir vorher nicht vorhersagen konnten.
NetLogo
NetLogo ist eine Programmiersprache und Simulationsumgebung speziell für Agent-Based Modelling. Die Webversion erlaubt uns, fertige Modelle direkt im Browser auszuprobieren.
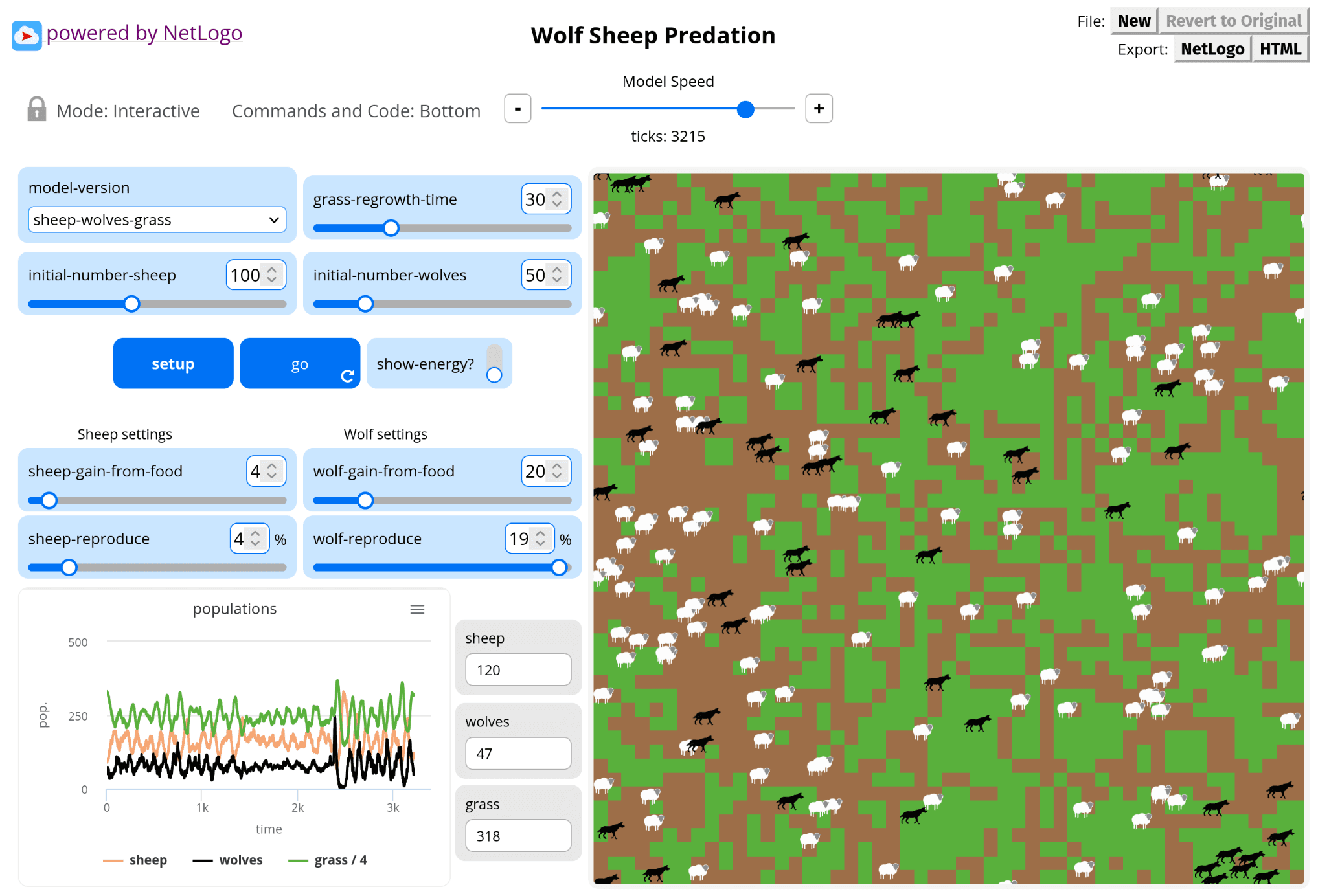
Teil 1: Wolf-Schaf-Gras Modell
In diesem ersten Modell simulieren wir ein klassisches Räuber-Beute-System mit drei Komponenten:
- Schafe (Beute): fressen Gras, werden von Wölfen gefressen
- Wölfe (Räuber): fressen Schafe
- Gras (Ressource): wächst nach, wird von Schafen gefressen
Das Modell verstehen
Öffnen Sie das Modell: Wolf Sheep Predation
Die Benutzeroberfläche
- Schwarze Fläche: Die “Welt”, in der die Simulation stattfindet
- Weisse Punkte: Schafe
- Braune Punkte: Wölfe
- Grüne Flächen: Gras
- Diagramme rechts: Zeigen Populationsgrössen über die Zeit
Die wichtigsten Parameter (Schieberegler)
| Parameter | Bedeutung |
|---|---|
initial-number-sheep | Startanzahl Schafe |
initial-number-wolves | Startanzahl Wölfe |
sheep-gain-from-food | Energie, die ein Schaf durch Gras gewinnt |
wolf-gain-from-food | Energie, die ein Wolf durch den Verzehr eines Schafs gewinnt |
sheep-reproduce | Wahrscheinlichkeit der Schaf-Reproduktion (%) |
wolf-reproduce | Wahrscheinlichkeit der Wolf-Reproduktion (%) |
grass-regrowth-time | Zeit, bis Gras nachwächst, nachdem es Schafe gefressen haben |
So funktioniert die Simulation
Pro Zeitschritt (“Tick”) passiert für jeden Agenten:
- Bewegung: Agent bewegt sich zufällig
- Fressen:
- Schaf auf grünem Feld → frisst Gras, gewinnt Energie
- Wolf auf Feld mit Schaf → frisst Schaf, gewinnt Energie
- Reproduktion: Mit gewisser Wahrscheinlichkeit entsteht ein Nachkomme
- Energieverlust: Bewegung kostet Energie
- Tod: Energie ≤ 0 → Agent stirbt
Wichtig: Modellwahl
Das Menü “model version” bestimmt, ob Gras als Ressource simuliert wird:
- mit Gras: Schafe brauchen Gras zum Überleben (3-Ebenen-System)
- ohne Gras: Schafe überleben ohne Gras (vereinfachtes 2-Ebenen-System)
Aufträge Teil 1 (ca. 35 Minuten)
Auftrag 1.1: Erste Erkundung (5 Min)
- Öffnen Sie das Wolf Sheep Predation Modell
- Stellen Sie sicher, dass Sie das sheep-wolves-gras-Modell ausgewählt haben
- Klicken Sie auf “setup”, dann auf “go”
- Beobachten Sie die Simulation und die Diagramme für ca. 1-2 Minuten
- Stoppen Sie die Simulation mit erneutem Klick auf “go”
Beantworten Sie:
- Was beobachten Sie im Diagramm? Gibt es ein Muster?
- Bleiben die Populationen stabil oder sterben Arten aus?
Auftrag 1.2: Das Gleichgewicht finden (10 Min)
Versuchen Sie, Parameter zu finden, bei denen beide Populationen aussterben.
- Starten Sie mit den Standardwerten
- Wenn eine Art ausstirbt, überlegen Sie: Was hat wohl zum Aussterben geführt?
- Notieren Sie Ihre Parameter
Tipps
- Wenn Wölfe zu schnell aussterben: Mehr Startschafe oder höhere Wolf-Energie pro Schaf
- Wenn Schafe aussterben: Weniger Wölfe, schnelleres Gras-Nachwachsen
- Wenn alles chaotisch ist: Kleinere Reproduktionsraten versuchen
Dokumentieren Sie: Welche Parameterkombination führt zu einem stabilen System?
Auftrag 1.3: Oszillationen untersuchen (10 Min)
In stabilen Systemen beobachten Sie oft Oszillationen (Schwingungen) der Populationen.
- Finden Sie eine Parameterkombination mit deutlichen Oszillationen
- Beobachten Sie das Diagramm genau
Beantworten Sie:
- Welche Population steigt zuerst - Schafe oder Wölfe?
- Was passiert danach mit der jeweils anderen Population?
- Erklären Sie den Zusammenhang in eigenen Worten
- Vergleichen Sie Ihre Beobachtung mit dem theoretischen Lotka-Volterra-Modell (Wikipedia)
Auftrag 1.4: Experimente (10 Min)
Führen Sie folgende Experimente durch und notieren Sie Ihre Beobachtungen:
Experiment A: Ohne Gras
- Wählen Sie das einfachere wolves-sheep-Modell
- Was ändert sich am Systemverhalten?
- Ist das System stabiler oder instabiler? Warum?
Experiment B: Überpopulation
- Wählen Sie wieder das wolves-sheep-gras-Modell
- Setzen Sie
initial-number-sheepauf 500 - Was passiert? Warum?
Experiment C: Räuber-Dominanz
- Verändern Sie
wolf-reproducewährend die Simulation läuft auf extreme Werte - Was passiert mit dem System?
Fassen Sie zusammen: Was haben Sie über die Wechselwirkungen im Ökosystem gelernt?
Teil 2: Evolution durch Selektion
Im zweiten Modell fügen wir einen wichtigen Aspekt hinzu: Vererbung und natürliche Selektion.
Das Konzept: Schrittgrösse und Vererbung
Im ersten Modell waren alle Schafe gleich und alle Wölfe gleich. Im neuen Modell hat jedes Tier eine individuelle Schrittgrösse (stride length):
- Grosse Schritte: Das Tier bewegt sich schneller, verbraucht aber mehr Energie
- Kleine Schritte: Das Tier bewegt sich langsamer, verbraucht aber weniger Energie
Der Trade-off:
stride-length-penaltyDer Parameter
stride-length-penaltybestimmt, wie viel Extra-Energie grosse Schritte kosten. Je höher dieser Wert, desto “teurer” ist schnelles Laufen. Das erzeugt einen Trade-off: Schnell sein hilft beim Finden von Futter (Schafe → Gras, Wölfe → Schafe), kostet aber Energie.
Diese Eigenschaft wird an die Nachkommen vererbt - mit kleinen zufälligen Variationen (Mutationen).
Natürliche Selektion und Selektionsdruck
Natürliche Selektion bedeutet: Individuen mit vorteilhaften Eigenschaften überleben und reproduzieren sich häufiger. Über viele Generationen “optimiert” sich die Population.
Der Selektionsdruck bestimmt, welche Eigenschaften vorteilhaft sind:
| Situation | Selektionsdruck | Vorteilhafte Schrittgrösse |
|---|---|---|
| Viele Wölfe, wenig Schafe | Wölfe müssen weit laufen, um Beute zu finden | Grössere Schritte (schneller Beute finden) |
| Wenig Wölfe, viele Schafe | Beute ist leicht zu finden, Energie sparen ist wichtiger | Kleinere Schritte (Energie sparen) |
| Wenig Gras | Schafe müssen weit laufen für Futter | Grössere Schritte |
| Viel Gras | Futter ist überall, Energie sparen lohnt sich | Kleinere Schritte |
Kernidee
Die Evolution “weiss” nicht, was gut ist. Es überleben einfach diejenigen Individuen, deren Eigenschaften zufällig zur aktuellen Umwelt passen. Über viele Generationen führt dies zu einer Anpassung an die Umweltbedingungen.
Das Modell verstehen
Öffnen Sie das Modell: Wolf Sheep Stride Inheritance
Neue Elemente in der Benutzeroberfläche
- Histogramme: Zeigen die Verteilung der Schrittgrössen in der Population
- Durchschnitts-Anzeigen: Zeigen die mittlere Schrittgrösse über die Zeit
Aufträge Teil 2 (ca. 35 Minuten)
Auftrag 2.1: Erste Beobachtung (5 Min)
- Öffnen Sie das Wolf Sheep Stride Inheritance Modell
- Klicken Sie auf “setup” und dann “go”
- Beobachten Sie die Histogramme der Schrittgrössen
Beantworten Sie:
- Wie verändern sich die Histogramme über die Zeit?
- Werden die Schrittgrössen grösser, kleiner, oder bleiben sie gleich?
Auftrag 2.2: Selektionsdruck bei Schafen (10 Min)
Untersuchen Sie, wie die Umweltbedingungen die Evolution der Schafe beeinflussen.
Szenario A: Wenig Gras
- Setup mit Standardwerten
- Setzen Sie
grass-regrowth-timeauf einen hohen Wert (z.B. 50) - Lassen Sie die Simulation 1000+ Ticks laufen
- Beobachten Sie die durchschnittliche Schrittgrösse der Schafe
Szenario B: Viel Gras
- Neues Setup
- Setzen Sie
grass-regrowth-timeauf einen niedrigen Wert (z.B. 10) - Lassen Sie die Simulation 1000+ Ticks laufen
- Vergleichen Sie mit Szenario A
Erklären Sie:
- In welchem Szenario entwickeln Schafe grössere Schritte? Warum macht das evolutionär Sinn?
- Welcher Selektionsdruck wirkt in jedem Szenario?
Auftrag 2.3: Selektionsdruck bei Wölfen (10 Min)
Untersuchen Sie nun die Evolution der Wölfe.
Szenario A: Wenig Beute
- Setup mit wenigen Schafen (
initial-number-sheep= 50) - Simulation laufen lassen, Wolf-Schrittgrösse beobachten
Szenario B: Viel Beute
- Setup mit vielen Schafen (
initial-number-sheep= 200) - Simulation laufen lassen, vergleichen
Beantworten Sie:
- Wie unterscheidet sich die Evolution der Wölfe in beiden Szenarien?
- Was ist der biologische Grund dafür?
Auftrag 2.4: Die Kosten grosser Schritte (10 Min)
Der Parameter stride-length-penalty simuliert, dass grosse Schritte mehr Energie kosten.
Experiment:
- Führen Sie drei Durchläufe mit unterschiedlicher
stride-length-penaltydurch:- Niedrig: 0.2
- Mittel: 0.5
- Hoch: 0.8
- Beobachten Sie jeweils, wie sich die durchschnittlichen Schrittgrössen entwickeln
Beantworten Sie:
- Bei welcher Penalty entwickeln sich die grössten Schrittgrössen?
- Erklären Sie den Zusammenhang zwischen Kosten und evolutionärer Anpassung
- Was bedeutet das für reale Ökosysteme? (Denken Sie an den Energieaufwand von schnellen vs. langsamen Tieren)
Auftrag 2.5: Reflexion (5 Min)
Vergleichen Sie die beiden Modelle und beantworten Sie:
- Was kann das zweite Modell zeigen, das im ersten nicht sichtbar war?
- Warum ist Agent-Based Modelling besonders geeignet, um Evolution zu simulieren?
- Nennen Sie eine Eigenschaft (ausser Schrittgrösse), die man in einem ähnlichen Modell untersuchen könnte.
Zusammenfassung
| Aspekt | Mathematisches Modell | Agent-Based Modell |
|---|---|---|
| Ansatz | Formeln für Gesamtpopulation | Simulation einzelner Individuen |
| Variation | Alle Individuen gleich | Jedes Individuum kann anders sein |
| Evolution | Schwer darstellbar | Natürlich integriert |
| Emergenz | Vorhersagbar | Überraschende Muster möglich |
Agent-Based Modelling erlaubt uns, komplexe Systeme zu verstehen, bei denen das Verhalten des Ganzen aus dem Zusammenspiel vieler einfacher Teile entsteht - genau wie in der Natur.